Apuntes de análisis y cálculo. E. Barrull, 1994.
- Introducción
- Función
- Definición
provisional
- Definición
- Gráfica de una función
- Límites
- Definición
provisional
- Definición
- Teoremas sobre límites
- Funciones continuas
- Intervalos finitos
- Definición de
función continua
Introducción
[El análisis matemático es la rama de la matemática que proporciona
métodos para la investigación cuantitativa de los distintos procesos de
cambio, movimiento y dependencia de una magnitud respecto de otras. Surge así,
de manera natural, en un período en el que el desarrollo de la mecánica y la
astronomía nacidas de los problemas de la tecnología y la navegación, habían
proporcionado ya un cúmulo considerable de observaciones, medidas e hipótesis
y estaban impulsando a la ciencia hacia la investigación cuantitativa de las
formas más sencillas de movimiento.
El nombre de 'análisis infinitesimal' no dice nada sobre el
objeto de estudio, sino que enfatiza el método. Se trata del método matemático
especial de los infinitésimos o, en su forma moderna, de los límites. (Aleksandrov,
1, 92)]
[Los matemáticos del siglo XVII se fueron percatando
gradualmente de que una gran parte de los problemas que surgían de distintos
tipos de movimiento (con la consiguiente dependencia de unas variables respecto
a otras), así como de problemas geométricos que no se habían podido abordar
con los métodos usuales, podían reducirse a dos tipos. Ejemplos sencillos de
problemas del primer tipo son: hallar la velocidad en cualquier instante de un
movimiento no uniforme (o, en general, encontrar la velocidad de variación de
una magnitud dada), y trazar una tangente a una curva dada. Estos problemas
condujeron a una rama del análisis que recibió el nombre de 'cálculo
diferencial'. Ejemplos muy sencillos del segundo tipo de problemas son:
encontrar el área de una figura curvilínea (el problema de la cuadratura), o
la distancia recorrida en un movimiento no uniforme, o, en general, el efecto
total de la acción de una magnitud continuamente variable. Este grupo de
problemas condujo a otra rama del análisis, el 'cálculo integral'. (Aleksandrov,
1, 95-6)]
[El problema del análisis es el estudio de las funciones, esto
es, de la dependencia de una variable respecto de otra. (Aleksandrov, 1, 103)]
Función
[El concepto más importante de todas las matemáticas es, sin
dudarlo, el de función: en casi todas las ramas de la matemática moderna, la
investigación se centra en el estudio de funciones. (Spivak, 47)]
[Los distintos objetos y fenómenos que observamos en la
naturaleza están orgánicamente relacionados unos con otros; son
interdependientes. El género humano conoce desde hace tiempo las relaciones más
sencillas de esta clase, y este conocimiento se halla expresado en las leyes físicas.
Estas leyes indican que las distintas magnitudes que caracterizan un fenómeno
dado están tan íntimamente relacionadas que algunas de ellas quedan
completamente determinadas por los valores de las demás... Fueron
correspondencias de esta clase las que sirvieron de origen al concepto de función.
(Aleksandrov, 1, 100)]
Definición provisional
[Una función es una regla que asigna a cada uno de ciertos números
reales un número real...
Una cosa, por encima de todo, debe quedar clara con estos
ejemplos: una función es una regla cualquiera que hace corresponder números
a ciertos otros números, no necesariamente una regla que pueda ser expresada
mediante una fórmula algebraica ...; ni tampoco necesariamente una regla a la
que sea posible encontrar una aplicación en la práctica. Más aún, la regla
puede prescindir de algunos números y puede incluso no estar del todo claro a
qué números se aplica la función... El conjunto de los números a los cuales
se aplica una función recibe el nombre de dominio de la función...
La práctica corriente consiste en designar una función
mediante una letra. Por razones obvias se emplea preferentemente la letra 'f
',
lo cual hace que sigan en orden de preferencia las letras 'g' y
'h', pero en fin
de cuentas puede servir cualquier letra (e incluso cualquier símbolo razonable)
sin excluir la 'x' y la 'y', si bien estas letras suelen reservarse para
designar números. Si f es la función, entonces el número que
f asocia con {el
número} x se designa por f (x); este símbolo se lee
'f de x' y se le da con
frecuencia el nombre de valor de f en
x...
..., si el dominio no se restringe explícitamente más, se
sobreentiende formado por todos aquellos números para los cuales la definición
tiene sentido. (Spivak, 47-50)]
Definición
[Una función es una colección de pares de números con
la siguiente propiedad: Si (a, b) y (a,
c) pertenecen ambos a la colección,
entonces b = c; en otras palabras, la colección no debe contener dos pares
distintos con el mismo primer elemento. (Spivak, 58)]
[La variable (dependiente) y es función de la variable
(independiente) x si existe una regla por la cual a cada valor de
x,
perteneciente a un cierto conjunto de números, corresponde un valor definido de
y (independientemente del modo en que se dé esta regla: mediante una fórmula,
una gráfica, una tabla o de cualquier otro modo (Aleksandrov, 1, 108)).
[El conjunto de los valores x que aparece en esta definición
se llama dominio de la función. (Aleksandrov, 1, 103)]
[Se dice que una variable y es función de otra
x,
cuando ambas están relacionadas de forma que para cada valor de x perteneciente
a su campo de variación le corresponde un {uno sólo} valor de y. La variable
y, cuyo valor depende del que tome x, recibe el nombre de variable
dependiente, mientras que x es una variable independiente. La relación
que liga a la función con la variable puede ser una tabla de valores en
correspondencia (por ej., una tabla de logaritmos), una gráfica o una ecuación.
(Ayres, 3)]
Gráfica de una función
[Puesto que una función no es más que una colección de pares
de números, el trazado de una función se reduce a trazar cada uno de los pares
de la misma. El dibujo así obtenido recibe el nombre de gráfica de la
función. En otros términos, la gráfica contiene todos los puntos
correspondientes a pares (x, f (x)). (Spivak, 72)]
[Una de las ideas más fructíferas y brillantes de la segunda
mitad del siglo XVII fue la de la conexión entre el concepto de función y la
representación geométrica de una curva. Esta conexión puede realizarse, por
ejemplo, por medio de un sistema de coordenadas cartesianas rectangulares. (Aleksandrov,
1, 103)]
Límites
[Entre todos los conceptos que se presentan en el cálculo
infinitesimal, el de límite es, a no dudarlo, el más importante, y quizás el
más difícil... lo que vamos a definir no es la palabra 'límite', sino la noción
de función que tiende hacia un límite. (Spivak, 99)]
[el análisis matemático moderno utiliza un método especial,
que fue elaborado en el transcurso de muchos siglos, y constituye ahora su
instrumento básico. Nos referimos al método de los infinitésimos o, lo que en
esencia es lo mismo, de los límites. (Aleksandrov, 1, 108)]
Definición provisional
[La función f tiende hacia el límite
l cerca de a, si se
puede hacer que f (x) esté tan cerca como queramos de
l haciendo que x esté
suficientemente cerca de a, pero siendo distinto de
a... solamente hace falta
que f (x) esté próximo a l cuando
x está próximo a a pero es distinto de a.
Sencillamente no nos interesa el valor de f (a) ni siquiera la cuestión de si
f (a) está definido. (Spivak, 99)]
Definición
[La función f tiende hacia el límite l en a
significa: para todo e >
0 existe algún d >
0 tal que, para todo x, si
 , entonces
, entonces
 .
.
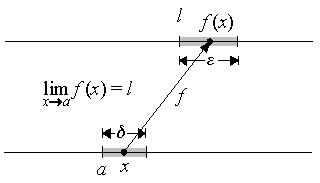
Esta función es tan importante (todo lo que emprendamos
a partir de ahora va a depender de ella) que sería en vano pasar adelante sin
saberla. ¡Apréndala el lector de memoria si es necesario, como si fuese un
poema! (Spivak, 110)]
[El número l al que tiende f cerca de
a se designa por
 (léase: el límite de
f (x) cuando
x tienda hacia a)... La ecuación
(léase: el límite de
f (x) cuando
x tienda hacia a)... La ecuación
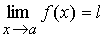
tiene exactamente el mismo significado que la frase
f tiende hacia l en
a.
(Spivak, 114)]
Teoremas sobre limites
Funciones continuas
[Intuitivamente, una función f es continua si su gráfica no
contiene interrupciones, ni saltos ni oscilaciones indefinidas. Aunque esta
descripción es, por lo general, suficiente para decidir si una función es
continua observando simplemente su gráfica, es fácil engañarse, y la definición
rigurosa es muy importante. (Spivak, 132)]
[Las funciones continuas constituyen la clase básica de
funciones para las operaciones del análisis matemático. La idea general de
función continua viene a ser la de que su gráfica sea continua; esto es, que
la curva pueda dibujarse sin separar el lápiz del papel. (Aleksandrov, 1, 117)]
Intervalos finitos
[Sean a y b dos números tales que
a < b. El conjunto de
todos los números x comprendidos entre
a y b recibe el nombre de intervalo
abierto de a a b y se escribe
a < x < b. Los puntos a y
b reciben el
nombre de extremos del intervalo. Un intervalo abierto no contiene a sus
extremos.
El intervalo abierto a < x < b junto con sus extremos
a y
b recibe el nombre de intervalo cerrado de a a
b y se escribe a
£
x £
b.
Sea a un número cualquiera. El conjunto de todos los números
x tales que x < a recibe el nombre de intervalo infinito. Otros
intervalos infinitos son los definidos por x
£
a, x > a y
x ³
a. (Ayres, 2)]
Definición de función continua
[La función f es continua en a si
 .
.
(Spivak, 132)]
[Una función se dice continua en un intervalo dado si
es continua en todo punto x de este intervalo...
Así, para dar una definición matemática de esa propiedad de
las funciones que viene caracterizada por el hecho de que su gráfica sea
continua (en el sentido usual de la palabra), fue necesario definir primero la
continuidad local (continuidad en el punto a), y luego, a partir de ella,
definir la continuidad de la función en todo el intervalo. (Aleksandrov, 1,
118-9)]